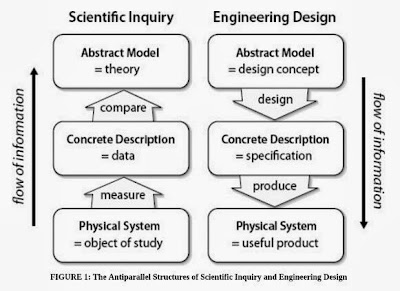
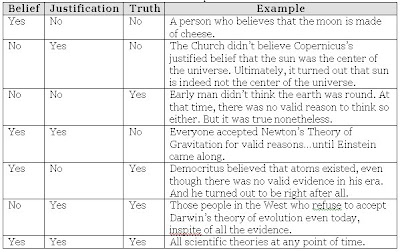
When One Door Closes, Others Open
In his book, Ignorance: How it Drives Science , Stuart Firestein wrote: “In science there are so far two well-known instances where knowledge is shown to have limits.” He was referring to the famous Uncertainty Principle from quantum mechanics and Gödel’s Incompleteness Theorem in maths. The former says it is impossible to know both items in certain pairs of properties of objects. What does Gödel’s Incompleteness Theorem say? Simply put, it about any system of axioms (statements taken to be true, as being “obvious” without a formal proof) and proofs built using those axioms. No matter how you much progress you make with this system, the theorem says that there will always be true statements that cannot be proven . Aha, you think, but does this just mean that one needs to add another fairly obvious axiom to the list? Would that then make all true statements provable? Go ahead, said Gödel, add another axiom to the list. I’ll then find a different true statement that can’t