Probability can be so Unintuitive


Probabilities can often be totally counter-intuitive. One of the easiest examples to describe is the Monty Hall problem, named after a game show by the same man:
1)      There are 3 closed doors. Behind one of them lies a big prize;
2)     You are asked to pick one. You do so, randomly of course;
3)     At this point, Monty Hall steps in. He opens one of the doors that you didn’t pick and reveals it to be empty. He offers you a choice: do you want to switch your choice to the other closed door or do you want to stick to the one you already picked?
Your intuition tells you that it doesn’t matter: 2 doors are still closed; so either choice has a 50-50 chance to win the prize, right?

Wrong! If you change your choice to the other closed door, you’d have 2/3 chance of winning whereas you’d have just a 1/3 chance by sticking to your original choice. How can that be?! And yet it’s true.

Ok, onto our next counterintuitive concept. If A beats B, and B beats C, then it follows that A beats C, right?

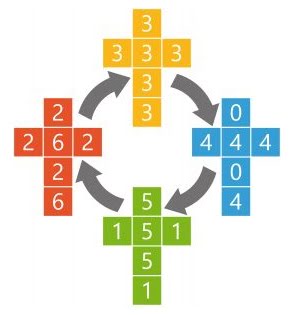
Not always. If you arrange the numbers on a dice appropriately, they don’t follow that seemingly obvious pattern. They’re called “non-transitive dice”:
In the pic above, each dice would beat the previous one in the loop on average!

At least the non-transitive dice is easy to see if you calculate the probabilities. But the Monty Hall problem is, as Tim Harford puts it, an “onion of a conundrum; layer after layer, and guaranteed to make you cry”.

Comments

  1. Ramiah KumarMarch 18, 2019 at 6:01 PM

    About the logic of "If A beats B, and B beats C, then it follows that A beats C, right?", one can more easily agree with "Not necessarily right". It happens so often is sports, where nearly equal teams compete. Probability theory need not defy common logic in a way here.

    About the previous question, for which the categorical probability declaration has been made thus: "Wrong! If you change your choice to the other closed door, you’d have 2/3 chance of winning whereas you’d have just a 1/3 chance by sticking to your original choice", doesn't seem to hold water. I just can't imagine why simply changing from the made-choice should change the probability.

    It's like this: a person makes a choice initially. The probability of 1/3 is fine, but there is this reality that the choice happened to be the Prize, just by fluke. Probability has already turned into the reality. That's certainly possible. Now, someone opens one of the not-selected boxes. Sure enough the prize is absent in that box. How can this truth be defied by any theory - probability or otherwise - "the prize is inside the selected box which is a reality. How can the prize shift to the other remaining box, as if some Masked Magician is fixing things here? Only if the choice was wrong by fluke, the treasure would be found in the remaining box.

    In other words, there is no reason why the probability of two boxes with one having the treasure should get invalidated at all, just because someone accidentally peeped into one of the two empty boxes and showed the content. At least I can't find a reason that favors the probability of 2/3. The situation looks like completely reset case: it's all new two boxes of which one has treasure. What's the probability trick then?

    ReplyDelete

Post a Comment

Popular posts from this blog

Student of the Year

Image
As a toddler, my daughter loved Alia Bhatt’s songs, esp. the ones from Student of the Year . (That movie did have many good songs and well-choreographed dances). Fast forward to present day, when she is 12 yo. She rarely watches Hindi movies now, but one of the few ones she likes of late, Raja aur Rani ki Prem Kahani has, yes, Alia Bhatt.   If I had any hopes that there was anything to be read in the name of her toddler-time favorite ( Student of the Year ), they have been dashed. Our conversations come exam time are perfectly captured by this photo and its caption: In fact, the pic below captures how she and I look at her answer sheets – me intently, she with an expression of “It’s over, so why are you even looking at it?”   Of late, we pull her leg and tell her that she isn’t showing any signs of academic prowess, she’d better find a rich guy to marry. Some time later, she showed us this meme on the Internet: “Me No Study, Me No Care Me Go Marry Millionaire If He Die
Read more

Animal Senses #7: Touch and Remote Touch

Instinctively, we think touch is based on contact. Not entirely true, explains Ed Yong in Immense World – there’s a more important aspect than contact: “These incredible feats are possible through movement. If you rest a fingertip upon a surface, you can get only a limited idea of its features. But as soon you’re allowed to move, everything changes. Hardness becomes apparent with a press. Textures resolve at a stroke.” As you run your fingers over a surface, they hit the tiny peaks and troughs and set off vibrations in the mechanoreceptors at their tips.   At the tip of its snout, the star-nosed mole has many pairs of hairless appendages. It uses them to touch things around itself. Alive or dead? Food or ignore? It does these movements at an insane speed. In the time it takes to blink our eyes, the star-nosed mole can probe, identify and swallow its food. “Light may be the fastest thing in the universe, but light sensors have their limits, and the star-nosed mole’s sense of
Read more

The Retort of the "Luxury Person"

Image
Coming up with biting and witty retorts. It’s something we dream of, but rarely manage to pull off. Worse, the more we stew over the offending remark, the more likely we are to come up with that dream retort, as Calvin ruefully points out: During our last holiday at the Taj Resort, seeing my wife carrying towels to our poolside chairs, one of the kids there mistook her for a member of the staff and asked for a towel. When my wife narrated this to us, I did not imagine that my 8 yo daughter would come up with her own retort. But a day later, my daughter recapped the incident, an incident that didn’t even involve her in the first place , and said, “You know what I’d have told that kid who asked for the towel?”. And without waiting for an answer, she told us anyway: “I don’t work here. I too am a luxury person who is living at this resort. Go get your own towel.” We were highly amused by the phrase she had coined: “luxury person”. It certainly captures the kind of holid
Read more